光学元件加工技术---- 第一章 光学理论分析
第一章 光学理论分析
广州斗龙光学科技有限公司(http://www.douloongoptics.com)非球面透镜生产工厂
光学系统是由透镜组合而成，本章主要叙述光的基本原理，透镜的几何光学成像理论，以及像差的问题，当中并以光学厂实际生产的镜头为例子，辅以印证理论。
1-1 基本原理
光是自然界的产物，以下就光的特性以及物理量加以说明。
1-1.1 可见光
可见光是电磁波谱之一部份，人的眼睛可视为是电磁波接收器，工作于此波段并依此定义出可见光。
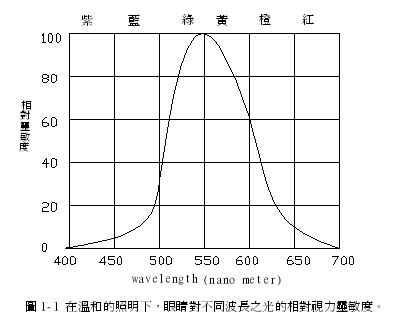
在光学中常用奈米(nanometer；1nm=1×10-9m)为波长单位，图 1-1显示可见光中心区域波长约为 550nm，颜色为黄绿色。视力灵敏曲线在长波长及短波长处渐趋近于轴。一般定视力灵敏度降至其最大值的1%处为极限，两极限的波长值分别约为 430nm 和 690nm。在此限度外之辐射若强度够的话，眼睛仍能探测到；若强度弱时，在许多物理实验中可用照相底片或感光灵敏之电子探测器代替人眼。
因光同时具有波和粒子的特性，一般物理现象的解释则采用适性策略：对于光的行进以电磁波解释，对于光的吸收与辐射，则以粒子特性来处理。
一般基础光学依光的性质和实验结果分为三类：
- 几何光学：将光视为粒子处理，但考虑的是整体特性表现，亦即对光的描述是用光线（ray）的集合－光束（light beam），以及物点、像点等概念。
- 量子光学：将光视为粒子处理，但探讨的是各别粒子本质。
- 波动光学：将光视为电磁波处理，本领域又称物理光学。
本论文研究的对象是精密光学组件，因此以几何光学为应用基础。
1-1.1 光源和光速
物体本身能发光的，如太阳、火焰、电灯、雷射称为光源（luminous source）。藉由光源照射物体而反射光线，方能使我们感觉物体的存在。光线可看做是由许多光子（photon）所组成，至于光束则是由许多光线汇集而成的光束线。
光在真空中，具有最大的速度，用符号 c 代表光在真空中的速度，是自然界的常数：c=299,792.5km/s≒30 万公里/秒。
1-1.2 光度与照度
光源的发光强度称为光度（luminous intensity）。以鲸油脂制成的蜡烛，每小时燃烧 120 格冷（1grain≒0.0648 克），所发出的光度，定为一国际烛光。
光源每单位时间所辐射出来的能量，为此光源之辐射通量，只有某小部份（波长从 400nm 到 700nm）的辐射通量能使人眼感觉其存在，此部份的辐射通量称之为光通量（luminous flux），单位为流明（lumen）。一标准烛光的光源，在一立体弧度角内所通过的光通量，称为一流明。
物体被照射时，在与光线垂直的表面上，单位面积所受到的光通量称为照度（illuminance），单位为流明/公尺2。
1-1.3 光的直线传播
在均匀的介质中，光前进的方式是以直线的方式而行，早期的针孔像机（pinhole camera）利用针孔成像的原理装成，足以证明光是直线前进的，观察像面上所成的像，是上下颠倒并且左右相反，像高与针孔至像面距离成正比关系，没有像差问题，且有相当程度的景深效果，如此看来针孔像机近似完美的光学系统，但是针孔非常地小，亮度却是一大问题，且分辨率将受限于绕射极限。
1-1.4 折射率
光学中折射率是一个非常重要的量，用符号 n 表示。介质折射率的大小定义成光在真空中的速度与光在介质速度中的比值
n＝ cv， …… ……………………………………. （1-1.1）
式中 n 表示折射率，c 表真空中之光速，v 表光在介质中之速度。
光在水中的速度是光速的四分之三，所以水的折射率约为 1.3，而一般光学玻璃的折射率约为 1.5，至于空气 n～1。折射率还有一个特性，介质中的折射率会随着光波波长而改变，这种关系也就是引起色散（dispersion）现象的原因。
1-1.5 光程
光程（optical path 简称 op）也是光学中一个非常重要的量，对一个均匀介质而言，它的定义是介质折射率 n 与实际光线所行走路径s 的乘积
op＝ns。 ………………………………………… （1-1.2）
若光所经过的是由 m 种不同折射率所构成的均匀介质层，那么光从 1 到 m 层介质的光程计算就应该是各层介质的折射率与实际路径乘绩的总和为
op＝1mi=∑nisi。 ……………………………………. 1-1.3）
如果光是在非均匀性的介质中行走，介质折射率就是一个位置的函数，光程计算相当于由起点(a)到终点(b)经过了多个不同折射率的介质层
op＝ban∫(s)ds。 …………………………………… （1-1.4）
1-1.6 色散
由于折射率是波长的函数 n(λ)，所以当一束复色光经折射后，因各单色光的折射率各不相同，造成折射方向有所差异，这种现象称为色散。色散能力ξ表示式如下
ξ＝1FDnncn ……………………………………….. （1-1.5）
式中Fn表蓝光（λ＝486.13nm）在介质 n 的折射率，nc 表红光（λ＝656.27nm）在介质 n 的折射率，以及Dn表黄光（λ＝589.29nm）在介质 n 的折射率。 然而对于一般玻璃而言，? 值约在 0.012~0.05 之间，数值较小使用上不方便，反而其倒数较常用来衡量介质的色散能力，一般称 ? 值倒数为 Abbe 数（Abbe number）Vd
Vd≡1v ＝1DFnnnc…………………………………….. （1-1.6）
Vd值约介于 20~80 之间，此值越小表示色散愈大。
1-1.7 光学玻璃
用于制造成透镜等光学组件的玻璃，特别讲究纯度和均匀度等性质，所以称为光学玻璃。描述光学玻璃有两个重要的参数为折射率Nd与 Abbe 数 VD。有了 ND值及 VD值，那么光学玻璃的光学特性就几乎完全掌握了。光学玻璃之材质务必兼顾到光学性质，物理性质，及化学性质。现分别叙述如下：
性能分为 a.光学性质：折射率、色散率、着色度。b.物理性质：比重。c.机械性质：硬度(耗损率)、冲击、弯曲率。d.热性质：转移点、软化点、线膨胀系数。e.电气性质：使用波长。f.化学性质：耐水性、耐酸碱性、耐风化性。
特性有 a.耐水性、耐酸碱性良好，即化学性质稳定。b.一般而言，折射率高者，耐酸性差，耐水性好，普遍来说材质含铅，所以比重较重。相反地，折射率低者，耐酸性好而耐水性差，比重较轻。c.研磨之难易度视光学玻璃被水侵蚀之快慢而定，耐水性差最易研磨，而耐水性良好即难研磨。d.耐化学性差之光学玻璃，较易研磨，但研磨面较易产生云雾霉状，或腐蚀。
品质定义为 a.依折射率与色散率而分，其种类共有两百多种。b.光学上之均匀性。c.光学公差，折射率△Nd：±0.00001~0.0001，色散率△Vd：±0.2~0.05%。d.脉纹、气泡与偏心。
1-2 光的波动性质
反射与折射是透镜成像的理论基础，用几何光学便可解释，但考虑绕射等性质时，需用波动概念，应用干涉原理，可以检查镜片的表面精度，所以本节将叙述光的波动性质。 1-2.1 反射与折射 图 1-2 显示空气中有一光束照于水面上，在水表面上产生反射现象，当其进入水中即发生折射，入射光与法线的夹角为入射角 θi，反射光与法线的夹角为反射角 θr，固定入射光的折射角度为 ?t，但改变波长，折射角度会随波长之增加而增加，短波长之光线偏折较大之角度，有较小折射角，图中 θ1表示红光（R），θ2表示绿光（G），θ3表示蓝光（B）之折射角度。
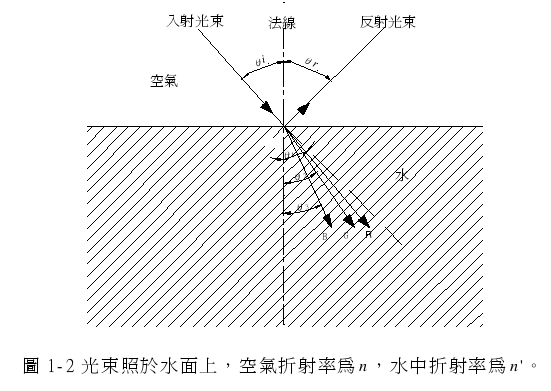
反射与折射定律定义为入射、反射与折射光在法线两侧，且与法线都在同一平面上。
入射角与折射角遵守斯涅尔（Snell）定律
nsinqi = n 'sinq t 。 …………………………………….. （1-2.1）
而入射角等于反射角qi =qr ，入射光束在光滑的表面会产生反射，但如在粗糙的表面则会产生漫射（diffuse reflection）现象，大半由于漫射之故，我们才能看到周围不发光的物体。
1-2.2 干涉 （Interference）
肥皂泡沫、油膜和其它薄膜的色彩是由于光的干涉所产生。
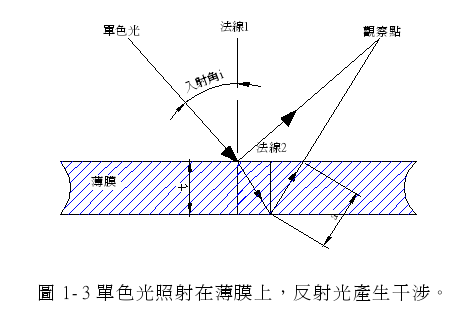
图 1-3 显示一均匀之薄膜，厚度为 t，折射率为 n。今有一单色光照射在薄膜上，其入射角为 i，则有一部份光被薄膜之上表面反射，进入观察点，另一部份光折射进入薄膜，被下表面反射，同样进入观察点，此两束光所经过之路程不同，进入薄膜之光线多走了 2a（如图所示）距离，但光在薄膜中之传播速率较空气中慢，故薄膜内单位长度之波数较空气中多，所以薄膜中 2a 之距离，相当于空气中 2na之距离，此称为光程长度，而光程长度差的大小决定光的干涉情况。
假设入射角 i=0，则 a=t（薄膜厚度），对一厚度为 t 之薄膜，其经上、下两表面反射后，在回至空气的两束光线，其光程长度差连同相改变λ/2 之和为
Y =2nt ＋l。 ………………………………………………. （1-2.2）
若此值为波长之整数倍，则有建设性干涉，而呈现明亮区，若此值为半波长之奇整数倍，则有破坏性干涉，而呈黑暗区。
上面是薄膜所反射的光之干涉情况，另外还有透过薄膜之光的干涉情况，如下图
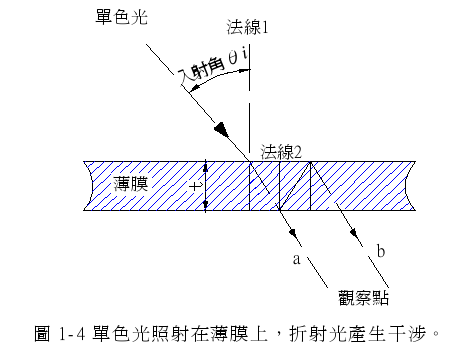
图 1-4 光束 a 连续穿过薄膜之两表面，光束 b 穿过薄膜之前，经上、下两表面各反射一次。光束 a 不经反射，故其波形与入射光相同，光束 b 经两次由薄膜至空气之反射，故波形亦不颠倒，故透过厚度为t 之薄膜的两光束，仅有光程长度差，而无相改变，假设入射角 i=0或甚小时，则光程长度差为
Y=2nt。 …………………………………………………（1-2.3）
同样的，若光程长度差为波长之整数倍，则两光束有建设性干涉，若此光程长度差为半波长之奇整数倍，则产生破坏性干涉。自薄膜反射之两光束比经薄膜透射之两光束多一相改变，即 Y 比 Y’多λ/2，故自薄膜上面见到的干涉条纹与自薄膜下面见到的干涉条纹正好相反。
1-2.3 衍射（Diffraction）
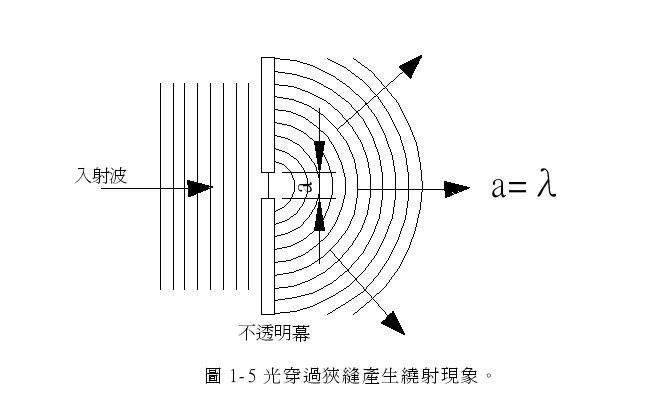
绕射是光在障碍物附近，如狭缝边缘的弯曲现象，镜头光学设计的 performance 有一定的极限，即受限于绕射的现象，称为绕射极限。
图 1-5 为入射波经过狭缝宽度 a＝λ时，狭缝外围产生亮度，即为绕射现象，当 a / ? 趋近于 0 时绕射现象益趋显著，减少狭缝宽度a 时绕射波变大，所以在实际光学系统中的孔径，如果小到某一程度，就会产生绕射现象。
由于绕射与干涉同样会产生条纹，但是条纹并不相同，表 3 是干涉条纹与绕射条纹之比较。
1-3 薄透镜系统
在光学的应用上，光学曲面比光学平面的应用要广泛的多，因为光学曲面除了和光学平面一样会造成光线方向的改变外，还能使光束产生发散（diverge），或会聚（converge）的现象，因而有不同的成像方式。
光学系统最常使用的组件，是将一块透明玻璃相对的两面磨成球面，一般统称为透镜(lens)，此外也可将透明塑料材料制成非球面透镜，透镜分类如下：
- 凸透镜(convex lens)，透镜中间部分较四周边缘厚者称之，图 1-6。
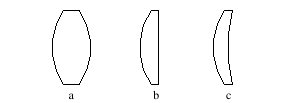
图 1-6 凸透镜形状 a.双凸透镜 b.平凸透镜 c.月凸透镜
凹透镜(concave lens)，透镜中间部分较四周边缘薄者称之，图 1-7。
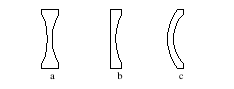
图 1-7 凹透镜形状 a.双凹透镜 b.平凹透镜 c.月凹透镜
1-3.1 成像公式
我们先对公式中所用到的符号加以定义及解释：
- 光线由左射向右，曲面左侧之距离定为负，右侧为正。
- 曲率（curvature）中心在曲面右侧者，其半径为正号。
- 若出射或入射于曲面的光线，转向法线（normal）为逆时钟方向，则该角度定义为负。
- 一般定光轴方向为 z 轴，像高方向为 y 轴，x 轴则与本文表面垂
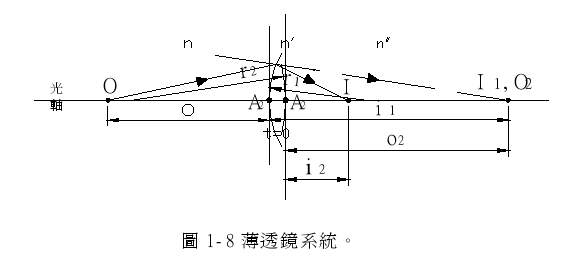
虽然薄透镜的厚度可以忽略不计，但基本上它仍然是由两个单一球面，中间夹着透明材料组成，所以对这样的系统成像就相当于做了两次单一球面成像，物对于第一球面所成的像（或像距），就相当于第二面的物（或物距）
1-5 光栏
在实际成像系统中会有下列问题：成像范围的限制，成像亮度的控制，这主要是系统中每一个光学组件的大小并非无穷大，会有某个范围的边缘限制，因而产生了成像范围及成像亮度的问题，这种具有边缘限制的组件都称为光栏，任何成像系统皆有光栏，如透镜的有效径(CA)或是外加的孔洞(多半是圆形)，照相机中可调孔洞直径的光圈(iris)，系统中可限制光通量且控制像亮度的光栏称为孔径光栏(aperture stop)。
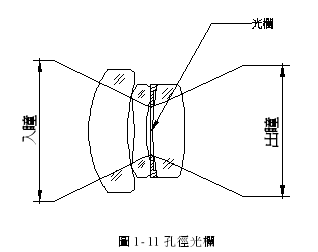
1-5.1 孔径光栏
图 1-11 是孔径光栏示意图，孔径光栏到底限制了多少光通量经由系统射到成像面上，先定义两个非常重要的面，一个在物空间观察到的孔径光栏称为入瞳（entrance pupil），入瞳的位置是将系统的孔径光栏对所有在它前面的成像组件所成的像，若孔径光栏前面没有组件那么孔径光栏本身就是入瞳，另一个是在像空间观测到的孔径光栏，称为出瞳（exit pupil），出瞳的位置是将系统的孔径光栏对所有在它后面的成像组件所成的像，若孔径光栏后面没有组件，那么孔径光栏本身就是出瞳，入瞳与出瞳可说是系统的入、出口，可能是虚的面(孔径光栏成的像)或是实际的面(孔径光栏)。
1-5.2 主光线和边缘光线(Chief ray & Marginal ray)
取离轴物点所发出的光线且此光线通过入瞳、孔径光栏、出瞳和光轴的交点，这条光线称为主光线。若由轴上物点所发出通过入瞳、孔径光栏、出瞳边缘的光线称为边缘光线。
1-5.3 决定亮度的物理量
这一节中要定义有关于系统亮度方面的物理量，有非常重要的特性和作用： 1.半视场角（half angular Field Of View）：半视场角ψ是物体对入瞳张角的一半，若ψ越大，则表示会有越多物体所发出的光线被聚集通过系统，也意味着光通量越大。 2.F/＃(F-number)：F/＃和系统的相对孔径及照速有密切关系，对较远物体的成像系统中(如照相机或望远镜的物镜… 等系统)，F/＃是个重要的物理量。当我们不考虑系统本身反射的能量和组件材料所吸收的能量，实通过系统的光能量将散布在有限的像面积上，成像面积越大则光通量密度就越小，因此系统上的光通量密度和成像面积是成反比的关系，然而成像面积又是正比于系统焦距的平方 1/f2 ，光通量的大小正比于系统孔径的面积，若以 D 代表入瞳的直径，则像面上的光通量密度就正比于 D2/f2， 我们将 D/f 的比值定义为系统的相对孔径，它的倒数则定义成
F/＃数值越小，像面上光通量密度越大，所以对照相机系统来说F/＃数值对曝光时间(快门速度)来说是个非常重要的物理量，F/1.4镜头的光通量密度是 F/2 的二倍，也就是说相同曝光量而言 F/1.4 镜头的快门速度要比 F/2 镜头快了两倍。
1-6 像差理论
评价光学系统的成像可以使用光线觅迹或像差理论来执行，光线觅迹对所追踪的光束给于正确结果，而像差理论则对系统的整个视场与孔径给于近似结果。
实际光学系统需考虑到物理光学的的绕射影响，还有为了亮度、视场等的要求，光线并非是近轴的轨迹，所成的像和理想像点会有出入，这种成像的缺陷就称为像差。连续光谱的像差为「色像差」，单一波长的像差为「单色像差」（monochromatic aberration）。
像差的产生有三种原因：1.绕射的影响。2.组件制造生产的公差(tolerance)要求。3.真实光线的几何光学结果。 将正弦函数sinq对q ＝0 作泰勒展开，得
当θ很小时，sinθ～θ
满足（1-6.2）式的光线就是高斯光学的近轴光线，又称第一阶光学理论(first order theory)，取展开式前面两项，称第三阶光学理论(third order theory)，取展开式前面三项，称第五阶光学理论(fifth order theory)，质量要求越高的成像系统，所讨论的阶数也越多。
1-6.1 球面像差(spherical aberration)
球差是指轴上物点发出的光线以不同高度入射至系统，通过系统后却无法会聚成像点的差异现象。球差会随物点的位置而改变，通常取平行于轴的光线（无限远的物点）入射至系统的情形为球差主值。
对一成像系统而言，要想完全消除大孔径透镜的球面像差是不可能的，但是我们可以利用下面的方法使透镜的球差减到最小：
- 使到达透镜第一面的光线角度与离开第二面的角度差不多相等，拿平凸透镜系统为例，以凸面对着物点时的球差就比平面对着物点的球差值来的小。
- 选择适当的透镜形状，可使透镜的球差最小，以薄透镜来说，相同焦距且相同材料的透镜，可以有不同的曲率半径，这些不同形状的透镜可以计算出不同的球差值。
- 将透镜的一面或两面磨成非球面，可以使此透镜的球差完全消除，然而非球面只能使某一物距的球差完全消除，其它的物距成像仍会有相当的球差存在。
- 要消除系统的球差，可以采用多透镜组合，利用各个透镜的正负球差相互弥补，使系统的总差值降低。
1-6.2 像散(astigmatism)
像散是离轴较远的物点因成像位置不同而造成的成像差异现象，一个有像散像差的系统中，离轴物点所发出的光线中，其子午光线（Tangential）成像位置和弧矢光线（Sagittal）成像位置不同，成像不会在同一点，成像的形状，在 T 位置上是一水平线，在 S 位置上是一垂直线，如图 1-12：
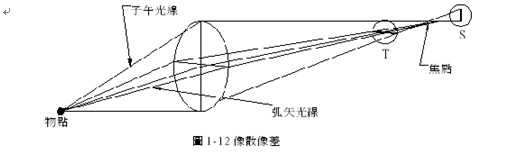
大体上来说，轴上的物点，是不会有像散像差发生的，物体离轴越远则像散像差越明显，由于产生像差的因素多半是离轴距离而造成，系统孔径的大小影响较小，所以一般我们多采用选择适当的透镜形状和适当的透镜间距来达成消除像散目的。
1-6.3 场曲(field curvature)
一平面物体不能够成像为一平面，而是成像为一曲面，即为像面弯曲，如图 1-13，此现象会使的画面周边画质模糊，缩小光圈也不能改善像面弯曲。
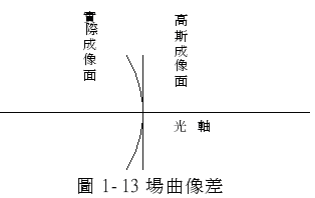
实务上，扫描仪镜头常会有场曲像差的问题，类似像散像差的改善方式，要减少场曲像差，也是选择适当的透镜形状和适当的透镜间距来达成，另外使用透镜厚度配对也是减少场曲的方法之一，实际的例子详见『第四章 4-3 场曲像差实务上的改善对策』。
1-6.4 畸变(distortion)
一条直线经过镜头拍摄后，变成弯曲的现象，称为畸变像差。
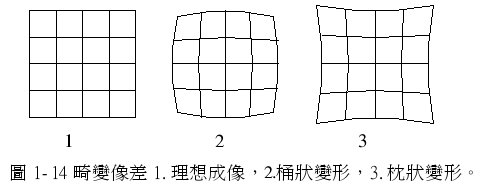
如图 1-14，向内弯的是「桶状变形」（Barrel），向对角线往外弯的是「枕状变形」（Pincushion），一支变焦镜头，通常在广角端呈现桶状变形，而在望远程呈现枕状变形。
1-6.5 色像差
透镜的成像系统中应用的基本原理是折射定律，因为折射率为波长的函数，不同波长的入射光会造成不同的折射角，所以造成成像有色差(chromatic aberration)产生。
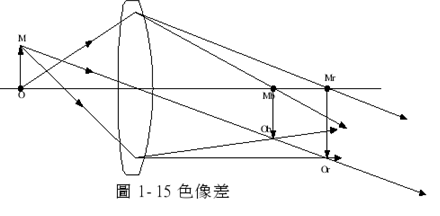
如图 1-15，轴上物点 M 对透镜成像，因透镜的折射率与波长成反比，使得各色光所成像点分开，红光的像点为 Mr，蓝光的像点称为纵向色像差，物成像会因光波长不同而有位置上的差异，成像的大小也会因不同光波长而有不同，的高度差就称为横向色像差。
若要消除色像差，通常是针对系统所使用的波长及需求来设计，若能矫正二个波长的色差并同时也矫正球差系统称为消色差透镜，一般来说最简单的消色差方法，是利用二种不同材料做成的胶合系统，其中一个透镜的正色像差和另一透镜的负色像差抵消，使得两特定波长的成像重合在一起。
若想以两个透镜的组合来消除色像差，除了上述的胶合系统外，还可采取分离式的设计。
